In problems where 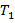 is a two dimensional temperature field is a two dimensional temperature field  the integral simplifies
to the integral simplifies
to
Since a path length difference of 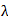 will generate one fringe shift, the temperature difference will generate one fringe shift, the temperature difference 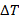 required for this purpose is required for this purpose is
In air  and in water, it is and in water, it is  . Since density decreases
with increasing temperature at constant pressure, both derivatives are negative under
normal conditions. . Since density decreases
with increasing temperature at constant pressure, both derivatives are negative under
normal conditions.
For  laser laser  . Hence . Hence  per fringe shift for a per fringe shift for a  laser is laser is  in air and in air and  in water. Note that the value in water. Note that the value 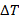 itself decreases
with increasing geometric path length itself decreases
with increasing geometric path length 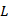 . Hence the sensitivity of measurements can be
adjusted by designing apparatus of varying dimensions in the direction of propagation
of light. In high temperature application L is made small while in problems involving
small temperature differences . Hence the sensitivity of measurements can be
adjusted by designing apparatus of varying dimensions in the direction of propagation
of light. In high temperature application L is made small while in problems involving
small temperature differences 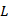 can be large. As discussed later, the largest value of can be large. As discussed later, the largest value of 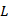 is, limited by refraction errors. is, limited by refraction errors.
In summary, each fringe of an interferometer represents a line of constant phase,
constant refractive index, constant density and hence constant temperature, namely an
isotherm. This aspect is useful in qualitative interpretation of interference patterns.
|