In a general setting, the material density will depend on pressure, temperature, and
species concentration. Interferometric measurements of temperature are possible when
pressure and concentration are either fully known, or, purely constant.
Consider a beam of light moving through a gaseous medium of varying temperature
and of total length 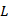 . . 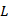 is also equal to the geometric path length traversed by the light
beam. The optical path length traversed by the light beam in the is also equal to the geometric path length traversed by the light
beam. The optical path length traversed by the light beam in the 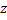 -direction, corrected
for changes in the light speed is -direction, corrected
for changes in the light speed is
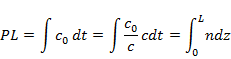
Here, 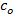 is the speed of light in vacuum, and is the speed of light in vacuum, and 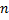 , the refractive index is defined as , the refractive index is defined as
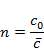
The integral is greater than 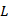 since since 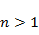 (except in absolute vacuum where (except in absolute vacuum where 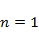 ). The
applicable coordinate system is shown in Figure 4.5. ). The
applicable coordinate system is shown in Figure 4.5.
Let beam 1 propagate through a region of variable density and hence refractive index, 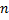 1 and beam 2 through a region constant density (and 1 and beam 2 through a region constant density (and 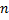 2). Then, the difference in path
lengths between 1 and 2 can be calculated as 2). Then, the difference in path
lengths between 1 and 2 can be calculated as
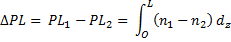
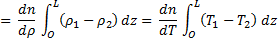
|
(6) |
|