| |
Data validation
In particle image velocimetry the measurements contain a number of spurious vectors.
These vectors deviate unphysically in magnitude and direction from the nearby vectors
that are, in turn, physically meaningful. They originate from those interrogation spots
that contains insuffcient number of particle images, or whose signal to noise ratio is
very low. In post processing process, the first step is to identify these 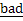 vectors and
subsequently discard them to form a valid data set. The detection of either a valid or
spurious displacement depends on the number and spatial distribution of particle image
pairs inside the interrogation spot. In practice, there should be at least four particle
image pairs to obtain an unambiguous measurement of the displacement (Westerweel, 2000). The number of particle images inside an interrogation spot is a stochastic variable
with a Poisson probability distribution. Hence an average of 10 particle images per
interrogation spot at an average in-plane displacement of vectors and
subsequently discard them to form a valid data set. The detection of either a valid or
spurious displacement depends on the number and spatial distribution of particle image
pairs inside the interrogation spot. In practice, there should be at least four particle
image pairs to obtain an unambiguous measurement of the displacement (Westerweel, 2000). The number of particle images inside an interrogation spot is a stochastic variable
with a Poisson probability distribution. Hence an average of 10 particle images per
interrogation spot at an average in-plane displacement of 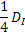 will give a probability of
95% of finding at least four particle image pairs. Here, will give a probability of
95% of finding at least four particle image pairs. Here, 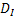 is the size of the interrogation
spot. The valid data yield can be improved by increasing the seeding density. But by
increasing the seeding density we increase the influence of the seeding on the flow. is the size of the interrogation
spot. The valid data yield can be improved by increasing the seeding density. But by
increasing the seeding density we increase the influence of the seeding on the flow.
There are various way to detect spurious vector in a velocity field. Three mainly
used tests are the global mean test, local mean test and local-median test. The global
mean and the local mean are both linear estimators of valid vectors. The local median test
is a nonlinear estimator that is often used in outliers identification. The outliers in turn,
are identified by the median of the sample data. Out of the above three, Westerweel [176]
has shown that the local median test has the highest effciency. In these techniques, the
value at a grid point is compared with the neighboring grid points; if it exceeds a certain
threshold, the value is discarded.
|