Evaluation of image pairs
Statistical evaluation technique is used to extract information of the displacement from
the two single exposed grey level patterns acquired at 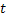 and and 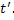 Statistical evaluation
technique is suitable since individual particle image pair detection is not possible for
high resolution PIV measurement. It is less sensitive to noise and image discretization
errors. In this technique, the whole image is sampled with an appropriate step size. For
each sampling location, a two dimensional grey level sample Statistical evaluation
technique is suitable since individual particle image pair detection is not possible for
high resolution PIV measurement. It is less sensitive to noise and image discretization
errors. In this technique, the whole image is sampled with an appropriate step size. For
each sampling location, a two dimensional grey level sample 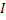 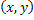 of certain shape and
size is extracted from the source image. It is cross correlated with the corresponding
sample of certain shape and
size is extracted from the source image. It is cross correlated with the corresponding
sample 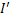 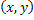 from the second image. from the second image.
In general, the cross-correlation function is given by
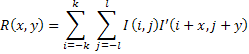
Here 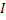 and and 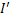 are intensity values of the image pair. The cross correlation function
produces a signal peak when the images align with each other, since the sum of the
product of the pixel intensities will be larger than elsewhere. are intensity values of the image pair. The cross correlation function
produces a signal peak when the images align with each other, since the sum of the
product of the pixel intensities will be larger than elsewhere.
In general, calculation of the correlation function is done in the Fourier space. For
FFT analysis the data should be periodic. There are other issues such as aliasing and
bias errors that need to be taken into consideration. Each subregion is transformed into
the Fourier space via a Fourier transformation. The sub-windows are the spatially shifted
and their Fourier transforms determined until the correlation is found. The correlation
values are weighted accordingly to reduce bias error.
The cross correlation of two functions is equivalent to a complex conjugate multiplication
of their Fourier transforms. In actual applications, the formulas used are
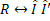
where 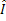 and and 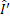 are the Fourier transforms of the image intensities are the Fourier transforms of the image intensities 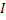 and and 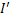 . .
|