The effective total time constant 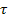 can be taken as the sum of the individual time constant can be taken as the sum of the individual time constant 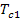 and and 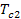 . This value has been plotted in Figure 2.26 as a function of the radius for three different lengths. As the radius . This value has been plotted in Figure 2.26 as a function of the radius for three different lengths. As the radius 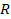 increases the viscous resistance to flow reduces faster than the increase in the fluid volume. Hence increases the viscous resistance to flow reduces faster than the increase in the fluid volume. Hence 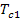 decreases with decreases with 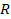 . In contrast to this it takes a longer time for the presence of the wall to be felt and . In contrast to this it takes a longer time for the presence of the wall to be felt and 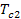 increases with increases with 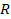 . At some intermediate radius ( . At some intermediate radius ( 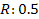 mm in Figure 2.25) the total time constant attains a minimum value. This radius as well as the magnitude of the total time constant depend on the length of the tubing. However Figure 2.26 shows that the effect of the length is not as pronounced as the radius. For a tube of radius greater than 2 mm the time constant is independent of the length and determined by mm in Figure 2.25) the total time constant attains a minimum value. This radius as well as the magnitude of the total time constant depend on the length of the tubing. However Figure 2.26 shows that the effect of the length is not as pronounced as the radius. For a tube of radius greater than 2 mm the time constant is independent of the length and determined by 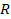 (and hence spatial variation) alone. (and hence spatial variation) alone.
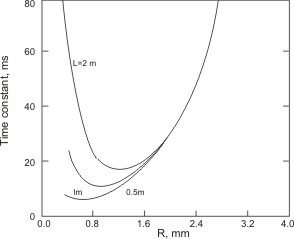
Figure 2.26: Time Constant of a Pitot Tube as a Function of Radius and Length. |
|