Physical Example of Unstable Calculation
Let us take the heat conduction once again
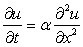 |
(8.10) |
Applying FTCS discretization scheme depict simple explicit representation as
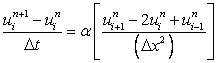 |
(8.11) |
or
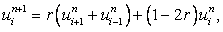 where where 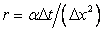 |
(8.12) |
This is stable only if 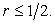
Let us consider a case when 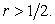 For r =1 (which is greater than the stability restriction), we get For r =1 (which is greater than the stability restriction), we get 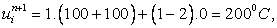 (which is impossible). The values of u are shown in fig 8.1. (which is impossible). The values of u are shown in fig 8.1.
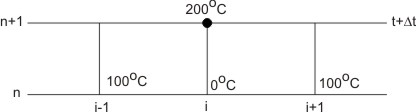
Figure 8.1: Physical Violations Resulting from r =1
Example demonstrating the application of Von Neumann method to multidimensional elliptic problems
Let us take the vorticity transport equation:
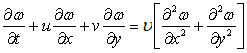 |
(8.13) |
We shall extend the Von Neumann stability analysis for this equation, assuming u and v as constant coefficient (within the framework of linear stability analysis). Using FTCS scheme
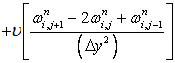 |
(8.14) |
Let us consider 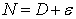 with with
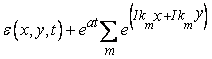 |
(8.15) |
where N is the numerical solution obtained from computer, D the exact solution of the FDE and ε is the error.
Substituting Eq. (8.14) into Eq. (8.13) and using the trigonometric identities, we finally obtain
where
where
The obvious stability condition 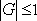 finally leads to finally leads to
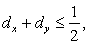 and and
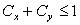 |
(8.16) |
when
which means
This is twice as restrictive as the one-dimensional diffusive limitation (compare with Eq. (8.9). Again for the special case 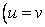 and and 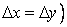
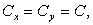 hence hence 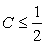 |
|
which is also twice as restrictive as one dimensional convective limitation (compare with Eq. (8.8).
Congratulations, you have finished Lecture 8. To view the next lecture select it from the left hand side menu of the page or click the next button. |