Stability of Hyperbolic and Elliptic Equations
Let us examine the characteristics of the first-order wave equation given by
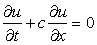 |
(8.3) |
Here we shall represent the spatial derivative by the central difference form
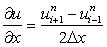 |
(8.4) |
We shall replace the time derivative with a first-order difference, where u(t) is represented by an average value between grid points 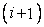 and and 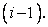 i.e i.e
Then
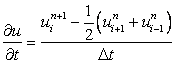 |
(8.5) |
Substituting Eqns. (8.4) and (8.5) into (8.3), we have
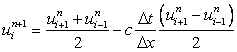 |
(8.6) |
The time derivative is called Lax method of discretization, after the well known mathematician Peter Lax who first proposed it.
If we once again assume an error of the form
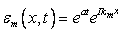 |
(8.7) |
As done previously, and substitute this form into Eq. (8.6), following the same arguments as applied to the analysis of Eq. (3.4), the amplification factor becomes
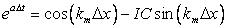 |
(8.8) |
where 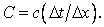
The stability requirement is 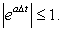
Finally the condition culminates in
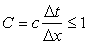 |
(8.9) |
In Eq. (8.9), C is the Courant number. This equation restricts 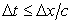 for the solution of Eq. (8.9) to be stable. for the solution of Eq. (8.9) to be stable.
The condition posed by Eq. (8.9) is called the Courant-Friedrichs-Lewy condition, generally referred to as the CFL condition.
|