| |
Similar expressions follow for the other cell faces. Combining Eqs. (41.4) and (41.5) yields a pressure-correction equation of the same structure as Eq. (39.12)
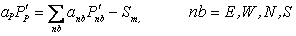 |
(41.9) |
where the source term 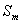 comes from Eq. (41.4), and the coefficients anb are: comes from Eq. (41.4), and the coefficients anb are:
The cross-derivatives have been omitted in flux corrections (e.g. 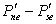 that would have appeared in expressions (41.8)). This reduces the pressure correction equation to a penta-diagonal one, which is relatively easy to solve. If, on the other hand, the full form of the corrections is taken into account, a nine-diagonal matrix is obtained. The expressions for the coefficients for such matrix are much more complex (see Peric, 1985). When the grid non-orthogonality is not severe (angle between grid lines in the range 450 to 1350 ), this simplification does not influence significantly the rate of convergence of the overall solution procedure. The final result is not affected by the simplifications introduced in deriving the pressure-correction equation, since this equation serves only to give corrections for the velocity and pressure fields. Finally at the , converged stage, all these corrections tend to zero. Hence, as long as the procedure converges, these simplifications are acceptable. that would have appeared in expressions (41.8)). This reduces the pressure correction equation to a penta-diagonal one, which is relatively easy to solve. If, on the other hand, the full form of the corrections is taken into account, a nine-diagonal matrix is obtained. The expressions for the coefficients for such matrix are much more complex (see Peric, 1985). When the grid non-orthogonality is not severe (angle between grid lines in the range 450 to 1350 ), this simplification does not influence significantly the rate of convergence of the overall solution procedure. The final result is not affected by the simplifications introduced in deriving the pressure-correction equation, since this equation serves only to give corrections for the velocity and pressure fields. Finally at the , converged stage, all these corrections tend to zero. Hence, as long as the procedure converges, these simplifications are acceptable.
Since the pressure-correction 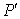 is derived from the continuity constraint, the corrected pressure and velocity components do not, in general, satisfy the momentum equations. Therefore, there is the possibility for further pressure corrections, similar to Issa's (1986) PISO algorithm, which can improve the momentum balance without destroying the achieved mass conservation. The use of such additional corrections, whose number can be specified by the user, is recommended in the case of highly non-orthogonal grids. Usually, one additional correction is sufficient. is derived from the continuity constraint, the corrected pressure and velocity components do not, in general, satisfy the momentum equations. Therefore, there is the possibility for further pressure corrections, similar to Issa's (1986) PISO algorithm, which can improve the momentum balance without destroying the achieved mass conservation. The use of such additional corrections, whose number can be specified by the user, is recommended in the case of highly non-orthogonal grids. Usually, one additional correction is sufficient.
In all correction steps, in order to stabilize the solution procedure, the pressure is corrected only by a fraction of 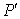 , i.e.: , i.e.:
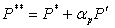 |
(41.11) |
The constant 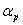 has a value between 0 and 1, and is called pressure underrelaxation factor. has a value between 0 and 1, and is called pressure underrelaxation factor.
|