| |
Velocities calculated from Eqs. (41.2) or (41.3) are deployed to calculate the mass fluxes F1 and F2 using Eq. (37.14). When substituted in the continuity equation (37.15), these fluxes leave a mass imbalance (“source”) 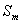 i.e.: i.e.:
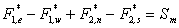 |
(41.4) |
Where the superscript “*” is used to denote the “uncorrected” values. Next, corrections are sought such that the corrected mass fluxes satisfy the continuity equation, i.e.:
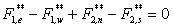 |
(41.5) |
where:
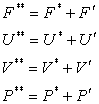 |
(41.6) |
Flux corrections, according to Eg. (37.14), result from velocity corrections, which are again linked to the pressure corrections in the spirit of the SIMPLE algorithm, e.g. (see Eq. (41.1)):
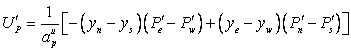 |
(41.7) |
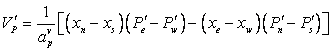 |
Corrections to the cell face velocities are derived in an analogous way, see Eqs. (41.3). in the flux expressions, however, the pressure difference across the face is dominating (in the above case 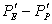 ), and in case of an orthogonal grid the contribution from the cross-derivatives would be zero (see Eq. (37.14)). (In the expression for the velocity components U and V two pressure gradients are always present, unless the grid is Cartesian.) By neglecting the cross-derivative terms, the flux corrections reduce to (for “e”-face): ), and in case of an orthogonal grid the contribution from the cross-derivatives would be zero (see Eq. (37.14)). (In the expression for the velocity components U and V two pressure gradients are always present, unless the grid is Cartesian.) By neglecting the cross-derivative terms, the flux corrections reduce to (for “e”-face):
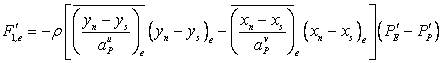 |
(41.8) |
|