For an iterative solution algorithm it is usual to write Eg. (39.11) for the central point P (Cell center) as:
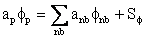 |
(39.12) |
Where "nb" denotes the neighboring nodes.
The coefficients 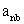 are are 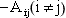 in Eg. (39.11). For the stability of an iterative solution method it is sufficient to have in Eg. (39.11). For the stability of an iterative solution method it is sufficient to have 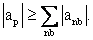 Whether this condition is satisfied, depends on the interpolation practice used to evaluate the convection terms (Ue, Un in Eqn (37.16)) and cross-derivative diffusion terms (Une, Use in Eqn (37.5)) Whether this condition is satisfied, depends on the interpolation practice used to evaluate the convection terms (Ue, Un in Eqn (37.16)) and cross-derivative diffusion terms (Une, Use in Eqn (37.5))
For faster convergence of the overall solution procedure, under- relaxation (Patankar, 1980) may be deployed. The change of the variable from one iteration to the next is multiplied by an under-relaxation factor 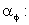
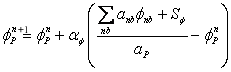 |
(39.13) |
where superscript n+1 and n denote new and old iteration levels, and 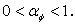 This can be arranged in a form equivalent with Eqn. (39.12) to yield: This can be arranged in a form equivalent with Eqn. (39.12) to yield:
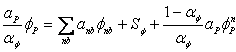 |
(39.14) |
where superscript n+1 has been omitted.
In the program, 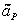 is simply taken to be is simply taken to be 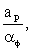 and and 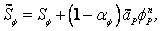 so that the structure of Eqn (39.12) is preserved. so that the structure of Eqn (39.12) is preserved.
The Coefficients 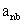 and and 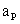 contain contributions of the convection and diffusion fluxes contain contributions of the convection and diffusion fluxes 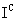 and and 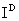 . Their exact form depends on the interpolation method for evaluating the CV face values of the dependent variables. . Their exact form depends on the interpolation method for evaluating the CV face values of the dependent variables.
Congratulations, you have finished Lecture 39. To view the next lecture select it from the left hand side menu of the page or click the next button. |