| |
Final Form of Discretised Equations
Invoking the flux components in discretized form and the discretized sources in Eqn. (37.11), one obtains an algebraic counterpart of the differential equation. The values of the dependent variables at the cell boundary location (e, w, n, s, ne, nw, se, sw) can be expressed in terms of nodal values; this gives an equation which provides a linkage between the node in the cell centre and the surrounding nodes. A system of M such equations, where M is the total number of control volumes, can be arranged in a matrix equation to read:
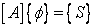 |
(39.11) |
where 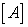 is a is a 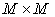 matrix, matrix, 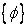 is the dependent variable vector of M nodal values, and {S} is a similar vector containing source terms. The matrix [A] is banded (i.e. it has non-zero coefficients only on some diagonals) if the values in the vector is the dependent variable vector of M nodal values, and {S} is a similar vector containing source terms. The matrix [A] is banded (i.e. it has non-zero coefficients only on some diagonals) if the values in the vector 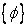 are arranged in a given order (e.g. along lines of constant grid index I from J=1 to JMAX, starting from I =1 to IMAX). A banded coefficient matrix makes the iterative solution easier. The solution algorithm recommended for these linear systems is Strongly Implicit Procedure (SIP) of Stone (1968). Other methods (such as BI-CGSTAB of Van der Vorst, 1992) can also be used and easily incorporated in the computer program. are arranged in a given order (e.g. along lines of constant grid index I from J=1 to JMAX, starting from I =1 to IMAX). A banded coefficient matrix makes the iterative solution easier. The solution algorithm recommended for these linear systems is Strongly Implicit Procedure (SIP) of Stone (1968). Other methods (such as BI-CGSTAB of Van der Vorst, 1992) can also be used and easily incorporated in the computer program.
|