Basic Aspects of Finite-Difference Equations
In this slide we shall look into some of the basic aspect of difference equations.
Consider the following one dimensional unsteady state heat conduction equation. The dependent variable 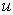 (temperature) is a function of (temperature) is a function of 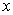 and and 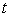 (time) and (time) and 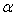 is a constant known as thermal diffusivity. is a constant known as thermal diffusivity.
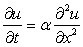 |
(3.3) |
It is to be noted that Eq.(3.3) is classified as a parabolic partial differential equation.
If we substitute the time derivative in Eq. (3.3) with a forward difference, and a spatial derivative with a central difference (usually called FTCS, Forward Time Central Space method of discretization), we obtain
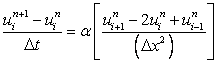 |
(3.4) |
In Eq. (3.4), the index for time appears as a superscript, where n denotes conditions at time 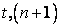 denotes conditions at time denotes conditions at time 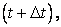 and so on. The subscript denotes the grid point in the spatial dimension. and so on. The subscript denotes the grid point in the spatial dimension.
However, there must be a truncation error for the equation because each one of the finite difference quotient has been taken from a truncated series.
Considering Eqns. (3.3) and (3.4) and looking at the truncation error associated with the difference quotients we can write
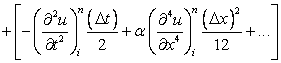 |
(3.5) |
In Eq. (3.5), the terms in the square brackets represent truncation error for the complete equation. It is evident that truncation error (TE) for this representation is 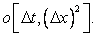
|