Combinations of finite difference quotients for partial derivatives form finite difference expressions for the partial differential equations.
Example, The Laplace equation 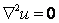 in two dimensions, becomes in two dimensions, becomes
or
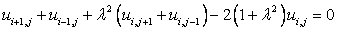 |
(3.1) |
Where 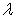 is the mesh aspect ratio is the mesh aspect ratio 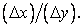
If we solve the Laplace equation on a domain given by Fig. 1.2, the value of 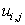 will be will be
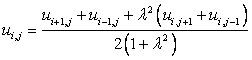 |
(3.2) |
It can be said that many other forms of difference approximations can be obtained for the derivatives which constitute the governing equations for fluid flow and heat transfer.
The basic procedure, however, remains the same. In order to appreciate some more finite difference representations see Tables 3.1 and 3.2.
Interested readers are referred to Anderson, Tannehill and Pletcher (1984) for more insight into various discretization methods.
|