Let us, for the present, consider a problem with no radiating boundary. Thus, the nodal equation for any of the nodes of the FEM can be constructed by appropriately summing up the contributions form the heat conduction term 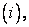 heat generation term heat generation term 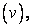 convective boundary terms convective boundary terms  and the heat flux boundary and the heat flux boundary 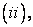 if the point lies on the if the point lies on the 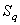 boundary. If the point lies on a known temperature boundary, the nodal equation is very simple, it takes the form boundary. If the point lies on a known temperature boundary, the nodal equation is very simple, it takes the form 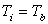 for the node for the node 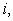 where where 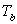 is the prescribed boundary temperature. is the prescribed boundary temperature.
The process of assembling all the contributions from the element in terms of nodal temperatures is done as follows. We try to obtain a global matrix equation in terms of nodal temperatures:
where 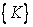 is conduction matrix and is conduction matrix and 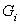 is the heat load vector. is the heat load vector.
The 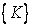 matrix is formed from the contribution of conduction resistances between the nodes of the triangular elements[Eq. (20.7)] and the convective resistance of the surface matrix is formed from the contribution of conduction resistances between the nodes of the triangular elements[Eq. (20.7)] and the convective resistance of the surface 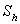 where the convective losses take place [Eq. (21.5)]. The heat load vector on the right hand side receives contributions from [Eq. (21.1) for each triangular element and heat flux through where the convective losses take place [Eq. (21.5)]. The heat load vector on the right hand side receives contributions from [Eq. (21.1) for each triangular element and heat flux through 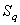 boundary [Eq. (21.4)]. The nodes falling on radiative boundary (term boundary [Eq. (21.4)]. The nodes falling on radiative boundary (term  in Eq. (19.1 ) requires special attention. in Eq. (19.1 ) requires special attention.
|