Elementary Finite Difference Quotients
Let us return to Eq. (2.1) and solve for 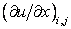 as: as:
or
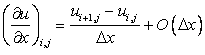 |
(2.4) |
In Eq. (2.4) the symbol 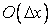 is a formal mathematical nomenclature which means “terms of order of is a formal mathematical nomenclature which means “terms of order of 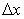 ” , expressing the order of the magnitude of the truncation error. The first-order-accurate difference representation for the derivative ” , expressing the order of the magnitude of the truncation error. The first-order-accurate difference representation for the derivative 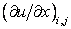 expressed by Eq. (2.4) can be identified as a first-order forward difference. expressed by Eq. (2.4) can be identified as a first-order forward difference.
Now consider a Taylor series expansion for 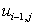 , and , and 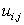
or
 |
(2.5) |
Solving for 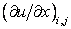 , we obtain , we obtain
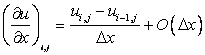 |
(2.6) |
Eq. (2.6) is a first-order backward expression for the derivative at grid point 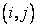
Subtracting Eq. (2.5) from (2.1)
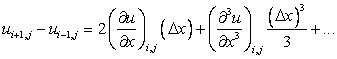 |
(2.7) |
And solving for 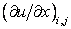 from Eq. (2.7) we obtain from Eq. (2.7) we obtain
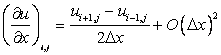 |
(2.8) |
Eq. (2.8) is a second-order central difference for the derivative 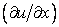 at grid point at grid point 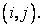
|