Elementary Finite Difference Quotients
Finite difference representations of derivatives are derived from Taylor series expansions. For example, if 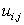 is the is the 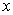 - component of the velocity, - component of the velocity, 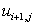 at point at point 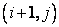 can be expressed in terms of Taylor series expansion about point can be expressed in terms of Taylor series expansion about point 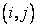 as as
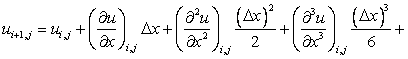 ... ... |
(2.1) |
Mathematically, Eq. (2.1) is an exact expression for 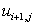 if the series converges. if the series converges.
In practice, 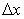 is small and any higher-order term of is small and any higher-order term of 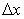 is smaller than is smaller than 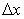 . Hence, for any function . Hence, for any function 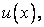 Eq. (2.1) can be truncated after a finite number of terms. Eq. (2.1) can be truncated after a finite number of terms.
Example:
In terms of magnitude, 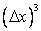 and higher order are neglected, Eq. (2.1) becomes and higher order are neglected, Eq. (2.1) becomes
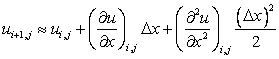 |
(2.2) |
Eq. (2.2) is second-order accurate, because terms of order 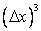 and higher have been neglected. If terms if order and higher have been neglected. If terms if order 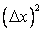 and higher are neglected, Eq. (2.2) is reduced to and higher are neglected, Eq. (2.2) is reduced to
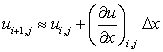 |
(2.3) |
Eq. (2.3) is first-order accurate.
In Eqns. (2.2) and (2.3) the neglected higher-order terms represent the truncation error. Therefore, the truncation errors for Eqns. (2.2) and (2.3) respectively are
and
It is now obvious that the truncation error can be reduced by retaining more terms in the Taylor series expansion of the corresponding derivative and reducing the magnitude of 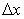 . .
|