An approximate evolution of Eqn. (15.5) would be
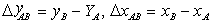 and and
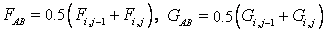
|
|
with similar expressions for 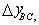 etc. If etc. If 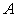 is not a Function of time, Eqn. (15.8) becomes is not a Function of time, Eqn. (15.8) becomes
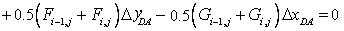 |
(15.8) |
For the irregular grid-mesh  the finite volume Eqn. (15.8) provides a discretisation in Cartesian coordinates without introducing generalized coordinates. If the grid-mesh is uniform and coincides with line of constant the finite volume Eqn. (15.8) provides a discretisation in Cartesian coordinates without introducing generalized coordinates. If the grid-mesh is uniform and coincides with line of constant 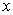 and and 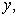 Eqn. (15.8) becomes Eqn. (15.8) becomes
or,
Which coincides with a central difference representation for the spatial terms of (15.1). The finite volume method, which is extensively used for both incompressible and compressible flows, has the advantages of conservative property.
Most importantly, it allows complex computational domains to be discretised in a simple way.
Congratulations, you have finished Lecture 15. To view the next lecture select it from the left hand side menu of the page or click the next button.
|