Equations with first derivatives
Here the finite volume method will be illustrated for the general first-order equation
|
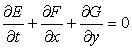
|
(15.1) |
where appropriate choices of E, F and G represent the various equations of motion. For example, for 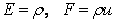 and and 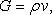 Eqn. (15.1) is the two-dimensional continuity equation and for Eqn. (15.1) is the two-dimensional continuity equation and for  , , 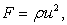 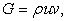 it is the inviscid momentum equation in the x-directions, and so on. it is the inviscid momentum equation in the x-directions, and so on.
In a similar manner, for x direction viscous momentum equation,
Assuming the finite volume (quadrilateral) ABCD shown in Fig. 15.1 is the representative of the control volume we consider the area integral of (15.1) over 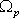 : :
Recall the Green's theorem
Applying Green's theorem, (15.3) becomes
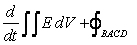 H.n H.n 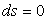 |
(15.5) |
where H 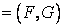 and and 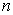 is the outward unit normal of segment is the outward unit normal of segment  (see Figure 14.5). For a segment (see Figure 14.5). For a segment 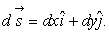 On a counter-clockwise contour, the outward unit normal On a counter-clockwise contour, the outward unit normal 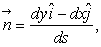 where where 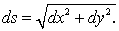 For the continuity equation, For the continuity equation, 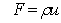 and and 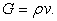
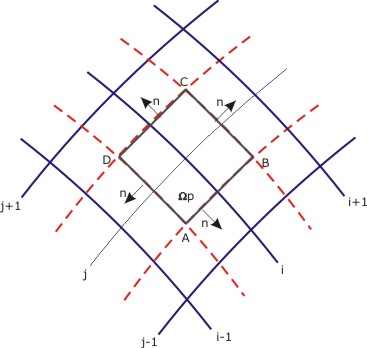
Figure 15.1: Finite Volume Mesh system.
In Cartesian coordinates,
H.n 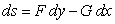
|
(15.6) |
Equation (15.5) is just a statement of conservation. For the particular choice, 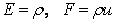 , , 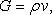 in Eqn. (15.5) concides with an integral statement of the conservation of mass. As mentioned, the finite volume method is a discretization of the governing equation in integral form, in contrast to the finite difference method, which is usually applied to the governing equation in differential form. in Eqn. (15.5) concides with an integral statement of the conservation of mass. As mentioned, the finite volume method is a discretization of the governing equation in integral form, in contrast to the finite difference method, which is usually applied to the governing equation in differential form.
|