Let us take non-conservative form of inviscid Burger's equation (9.11) as
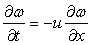 |
(10.5) |
Using FTCS differencing technique as before, we can write
 |
(10.6) |
Now, the integration over 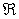 running from running from 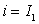 to to 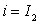 , yields , yields
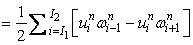 |
(10.7) |
While performing the summation of the right-hand side of Eq. (10.7), it can be abserved that terms corresponding to inner cell fluxes do not cancel out. Consequently an expression in terms of fluxes at the inlet and outlet section, as it was found earlier, could not be obtained. Hence the finite-difference analog Eq. (10.6) has failed to preserve the integral Gauss-divergence property, i.e. the conservative property of the continuum.
The quality of preserving the conservative property is of special importance with regards to the methods involving finite-volume approach (a special form of finite-difference equation).
|