Let us consider inviscid Burger's equation ((9.11)).
This time we let 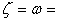 vorticity, which means vorticity, which means
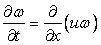 |
(10.1) |
The finite difference analog is given by FTCS method as
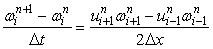 |
(10.2) |
Let us consider a region 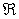 running from running from 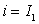 to to 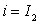 see (Figure10.1). see (Figure10.1).

Figure 10.1: Domain running from 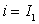 to to 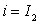 . .
We evaluate the integral 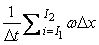 as as
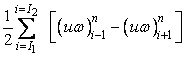 |
(10.3) |
Summation of the right hand side finally gives
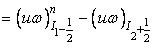 |
(10.4) |
Eq. (10.4) state that the rate of accumulation of 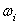 in in 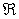 is identically equal to the net advective flux rate across the boundary of is identically equal to the net advective flux rate across the boundary of 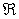 running from running from 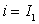 to to 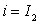 . .
Thus the FDE analog to inviscid part of the integral Eq. (10.2) has preserved the conservative property. As such, conservative property depends on the from of the continuum equation used.
|