Module 3 : Programmable Logic Devices (PLDs)

Lecture 2 : Introduction to microprocessor programming

In this lecture we will study the various number systems, programming languages, and internal architecture of the basic microprocessor, 8085 .

1. Number System

Number system is a way of representing the value of any number with respect to a base value. Number System can be classified on the basis of its “base”. Each number has a unique representation in a number system. Different number systems have different representation of the same number . In general Binary, Octal, Decimal and Hexadecimal Number systems are used in microprocessor programming. Table 3.2.1 shows different numbering systems and their details.

Table 3.2.1 Numbering systems

1.1 Number representation

1.1.1 Conversion of any number system to decimal number system:

Let B be the base of number system and An, An-1, …………………A1, A0 be the digits of given number. Then to convert it into decimal equivalent we can use the following formula:

N = An.Bn + An-1.Bn-1 + ……….+A1.B + A0.B0                                                                                                                                      (3.2.1)

Example: what is the decimal equivalent of (11101011)2 ?

  Here, we have taken An = 1, An-1 = 1, ……. An-3 =0, while n=8 and B = 2.

Then the decimal equivalent is (235)10 .

1.1.2  Decimal number system to any number system:

Any number in decimal system can be changed to any other number system by continuously dividing it by base of the required number system and then writing remainders after each step in reverse order.

Let us take an example of converting a decimal number 235 to its binary equivalent. Following table shows the conversion process as stated above.

Table 3.2.2 Binary representation of (235)10

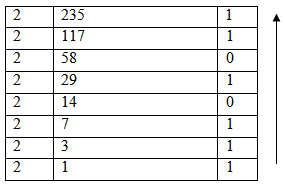
→ Hence Binary equivalent of (235)10 is (11101011)2.

1.1.3 Hexadecimal system

This system is quite extensively used in microprocessor programming. It facilitates much shorter representation of number in comparison with that obtained by using the binary number system. Hexadecimal system has a base of 16 and it is easy to write and remember the numbers and alphabets viz. 0 to 9 and A to F. Table 3.2.3 shows numerals and alphabets used in hexadecimal system for representation of a number.