where L is the length of the curve and yc is the centroidal coordinate of the curve. But 2pyc is the circumferential length of the circle formed by having the centroid of the curve rotate about the x-axis. This proves the theorem.
Second theorem:
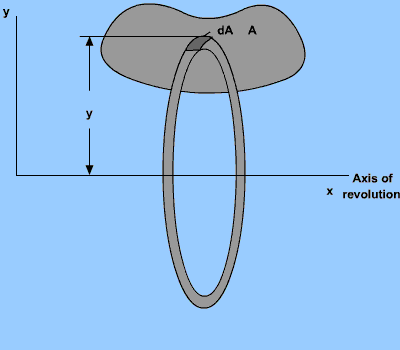
Consider a plane surface and an axis of revolution coplanar with the surface but oriented such that the axis such that the axis can intersect the surface only as a tangent at the bounding or have no interaction at all. The volume of the body of revolution developed by rotating the plane surface about the axis of revolution equals the product of the surface times the circumference of the circle formed by the centroid of the surface in the process of generating the body of revolution.
Proof:
Consider a plane surface A as shown in the figure. The volume generated by revolving dA of this surface about the x-axis is