Theorem of Pappus- Guldinus:

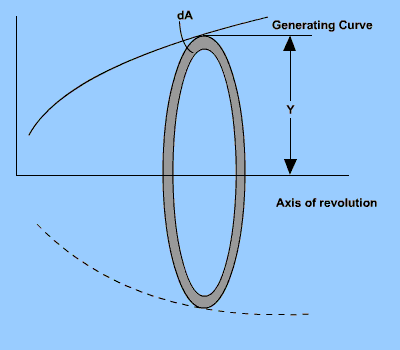
Consider a coplanar generating curve and an axis of revolution in the plane of this curve. The generating curve can touch but must not cross the axis of revolution. The surface of revolution developed by revolving the generating curve about the axis of revolution has an area equal to the product of the length of the genearating curve times the circumference of the circle formed by the centroid of the generating curve in the process of generating a surface of revolution.

Proof:

Consider an element dl of the generating curve. For a single revolution of the generating curve about the x-axis , the line segment dl traces an area dA = 2pydl

For the entire curve, this area becomes the surface of revolution given as