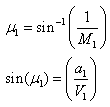23.1 Comparison of Shock Wave and Mach Wave
Consider a supersonic flow over a wedge as shown in Fig. 23.1. This wedge makes an angle ![]() with the upstream or freestream flow.
with the upstream or freestream flow.
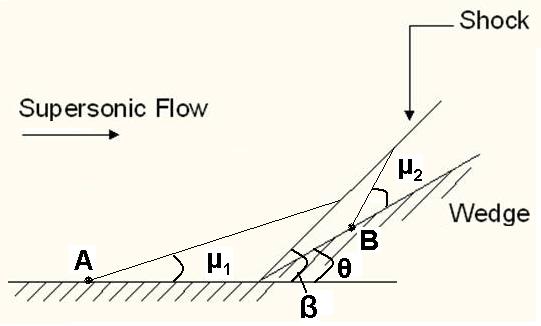
Fig. 23.1 Supersonic flow over wedge
The shock originated from the corner of the wedge makes an angle shock angle β with the upstream or freestream flow. We have already seen that the components of velocity upstream of the shock can be expressed as
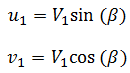
where, u1, v1 are components of upstream velocity in the direction normal and parallel to the shock. Hence we can express the shock angle as,
|
23.1 |
Consider a Mach wave oriniating from any point A upstream of the shock. For this Mach wave we have,
|
|
where µ1 is the angle made by the Mach wave with the local velocity vector. Comparing equation (23.1) and (23.2) we get, β > µ1 since µ1 > a1 (component of upstream velocity normal to the shock is always supersonic). This expression also portrays that shock angle is always greater than the Mach angle or angle made by the Mach line.
23.2 Proof for the interaction of shocks of same family.
Initially we will prove that two shocks of same family intersect each other if they are originated from the same double wedge conifiguration. Therefore consider the same situation as displayed by the Fig. 23.1.
Lets express the post shock conditions as,
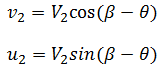
Hence,
|
23.3 |
Consider a Mach wave oriniating from any point B downstram of the shock. For this Mach wave we have,
|
23.4 |
where, u2, v2 are components of downstream velcoity in the direction normal and parallel to the shock and µ2 is the angle made by the Mach line with the local velocity vector which is presently the slant face of wedges.Comparing equations (23.3) and (23.4) we can see that (β - θ) < µ2 since it has been already proved that the compenent of downstream velocity normal to the shock is subsonic, hence µ2 < a2. Therefore both (upstream and downstream) Mach lines or waves intersect with the shock. Now cosider the supersonic flow over double wedge as shown in Fig. 23.2. In this way we can prove that the two shock originating from two corners of wedges given in Fig. 23.2 should intersect with each other. The main reason behind this interaction is that the downstream Mach line intersects with the first shock. It is also known to us that the shock angle is always greater than the local Mach angle, therefore the next shock angle will be necessarily greater than µ2. This logical derivation proves the fact that two shock of same family should intersect with each other for the double wedge configuration.
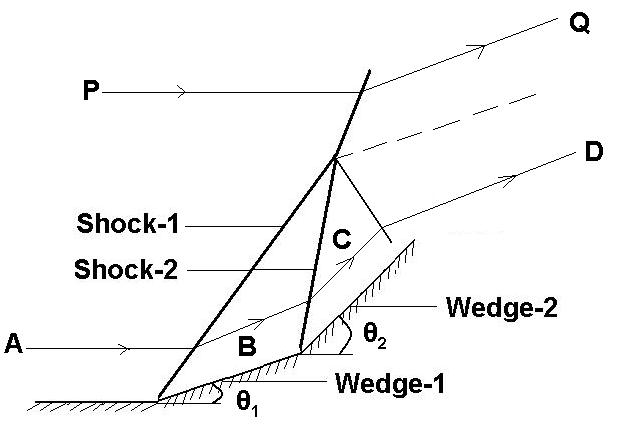
Fig. 23.2. Shock-Shock interafction for same family shocks