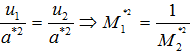Consider an ideal case where flow is decelarated from sonic condition to stagation conditions. The one dimensional relation when applied to this case give following relations. Here, we will use a superscript '*' for this special condition named as stared conditions represented by sonic speed. Hence the ratios for temperature, pressure and density in terms of stagnatiyon to static propertis at sonic condionns are as,

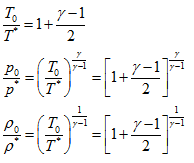
Since specific heat ratio for air is 1.4, above equations can be modified for air as

3.6. Normal shock relations

It had already been discussed that the subsonic flow is pre-warned and supersonic flow is not. The reason behind this fact is that, any small amplitude disturbance travels with acoustic speed, however speed of fluid particle is more than the speed of sound in case of supersonic flows. Therefore the message of presence of the obstacle can not propagate upstream. Hence a messenger gets developed in front of the obstacle to warn the flow in order to avoid its direct collision with the obstacle. This messenger is called as shock. In the presence of normal shock, fluid velocity decreases to the extent where flow Mach number behind the shock attains value below one. Due to this subsonic speed attainment of the flow, it becomes aware about the presence of the obstacle well in advance in the narrow space between shock and obstacle. Herewith we will deal for computation of flow properties behind the normal shock.

In the presence of a general obstacle the shock pattern is shown here in Fig. 6.2.

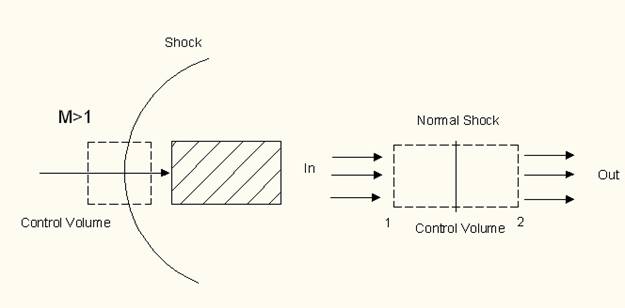
Fig. 6.2. Shock pattern for a blunt or bluff obstacle

The shock for the stagnation streamline can be considered as normal to it. Therefore we can use the earlier derived 1D flow relations along with the assumptions of flow steady, adiabatic and inviscid flow. Consider a small control volume around normal shock for application of these relations between two stations of the control volume, mainly, inlet and outlet as shown in Fig. 6.2.

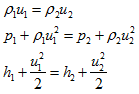
Lets us examine the reference star properties of the flow in the process to calculate the flow properties behind the normal shock from the known inlet conditions. We can take the advantage of using stared temperature since the flow is adiabatic in nature. Imagine that flow is adiabatically brought to Mach number one on either sides of the shock independantly. In this case, we should get same stared temperature on either sides of shock. We can also show that total temperature is also same on either sides. The explicit formulation using the star temperature and concerned acoustic speed before the normal shock is,

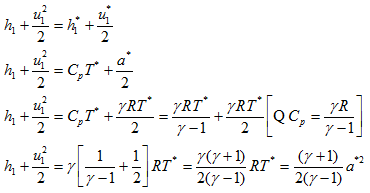
Applying same strategy at the outlet we get,

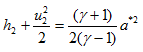
However, we can write static enthalpy in terms of acoustic speed as,

Therefore, the energy equation at the inlet becomes,

6.4

Similarly for the outlet station we have

6.5

Let's obtain the expression for velocity using mass and momentum equations to replace the acustic speed term from equations (6.4) and (6.5).

From 1D mass and momentum conservation equations we have

ρ₁u₁ = ρ₂u₂
p₁ + ρ₁u₁² = p₂ + ρ₂u₂²

Therefore,

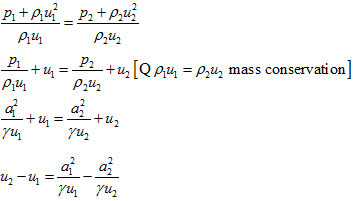
Using equation 6.4 and 6.5, above equation transforms to

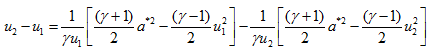
Rearranging the terms of above equation, we get

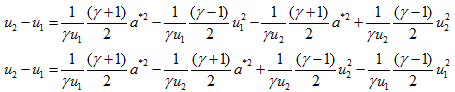
Further rearrengments gives

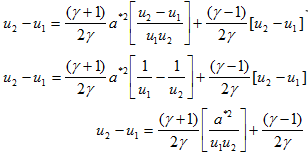
Necessary rearrangement for the above equation is as given,

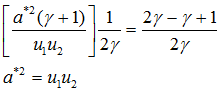
6.6

This expression shows that, M₁^*2 and M₂^*2 are reciprocal of each other for a normal shock. This equation is called as Prandtl’s relation for normal shock which can be used to prove that Mach number becomes subsonic behind the normal shock