12.2 Analysis of Critical Points of Rayleigh Curve

The same conservation equations for 1D heat addition can be re-written in differential form as,

For mass conservation equation

ρu = const = k

d(ρu) = 0                         Mass Conservation
or

For momentum conservation equation

P + ρu² = const

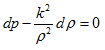                        Momentum Conservation

For energy conservation equatuon

dh + udu = dq                        Energy Conservation
P + vk² = const

From laws of thermodynamics,

Tds = dh - vdp

However for point 3 (where Rankine line is tangent to an isotherm) dh=0 or dT=0, hence.

Tds = - vdp

From energy equation, for the same point we have,

Tds = udu

Hence,

- vdp = udu

Using differential form of mass conservation equation, we can replace du and we get,

12.2

However, we know that point 3 also lies on an the isotherm, we can calulcate the slope of the isotherm to obtain another expression for as,

Hence we can put this in equation (12.2),

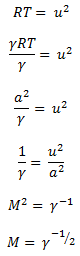
This procedure provides a fomal proof for the Mach number at the point which corresponds to maximum temperture on Rayleigh curve. This expression also proves the fact that upper brach of Rankine curve (Fig. 12.2) in h-s diagram corresponds to subsonic flow.

Similarly we can also prove that the sonic point (M=1), represented by point 4, corresponds to maximum entropy.

We know the momentum conservation equation as
p + vk² = const
The differential form of the same can be written as
dp + k²dv = const
Hence slope of Rankine line on p-v diagram is


We know that, at the point of maximum entropy, Rankine line is tangent to the isentrop. Hence slope of the isentrop at point 4 is
pv^γ = const
Differentiating this equation we get
v^γdp + pγv^γ-1dv = 0

Equating the slopes we get,

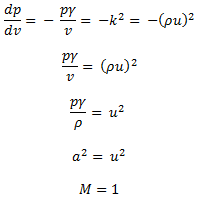
This expression proves the fact that maximum entropy point on Rayleigh curve corresponds to Mach number 1 or sonic condition. We can extend our analysis about heat addition in subsonic flow and attainment of maximum entropy as follows.

We know that addition of heat increases the total temperature and hence total enthalpy of the flow .

We know that,


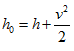
Hence the differential form of this equation is,
dh₀ = dh + udu

However added heat gives rise to this change in total enthalpy, hence
dq = dh₀

But dq = Tds. Therefore
Tds = dh₀ = dh + udu

However at the maximum entropy point, ds = 0 , therefore dh₀ = 0. Hence we can conclude that, maximum entropy point also corresponds to maximum total enthalpy and hence total temperature point. Therefore further addition of heat is not possible for the given mass flow rate. Hence point 4 also represents the chocking condition. Change in upstream conditions take place if we add heat more that the heat reqired to chock the flow.