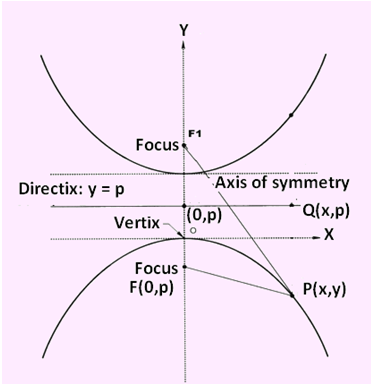
A hyperbola is mathematically defined as the set of points in a plane whose distances from two fixed points called foci, in the plane have a constant difference.

 

Constructing a Hyperbola
 Hyperbola can also be construct if the distance between Foci and Distance between vertices are known. This is illustrated in figure 4.
Draw  the axis of symmetry and construct a perpendicular through the axis.  Locate focal point F equidistant from the perpendicular and on either side of it.  Locate points A and B on the axis equidistant from the perpendicular. 
AB is the distance between vertices.
With F as center and radius R1, and draw the arcs.  With R1 + AB, radius, and F as center, draw a second set of arcs. The intersection of the two arcs on each side of the perpendicular are points on the hyperbola.

Select a new radius R2 and repeat step 2. Continue this process until several points on the hyperbola are marked

 

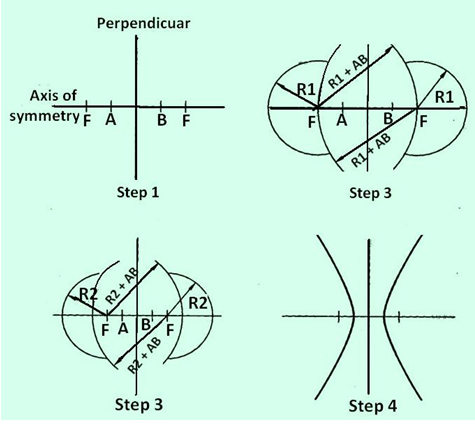
                   Figure 4. Construction of a hyperbola