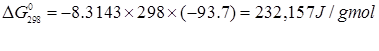Molar Gibbs function of an ideal gas at temperature T and pressure p is given by
|
(3.74) |
For the reaction of the type
|
(3.75) |
The Gibbs function change of the reaction ΔG is defined by the expression
ΔG = v3g3 + v4g4 - v1g1 - v2g2 |
(3.76) |
where the g's refer to the gases completely separated at T, p, ΔG is also known as the free energy change. Substituting the values of the g's
|
(3.77) |
But
ln K = -(v3Φ3 + v4Φ4 - v1Φ1 - v2Φ2) |
(3.78) |
|
(3.79) |
If p is expressed in atmospheres and ΔG is calculated from each gas is at a pressure of 1 atm, the second term on the right drops out. Under these conditions ΔG is known as the standard Gibbs function change and denoted by ΔG0
|
(3.80) |
This is an important equation which relates the standard Gibbs function change with temperature and the equilibrium constant. From this the equilibrium constant can be calculated from changes in the changes in the standard Gibbs function, or vice versa. For dissociation of water vapour,
|
(3.81) |
ln K298 = - 93.7
Therefore,
|
(3.82) |
Substituting ln K from Nernst’s equation
|
(3.83) |
from which also ΔG0 may be calculated directly. Values of 
for fundamental
ideal gas reactions are given in Table 3.3