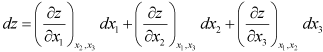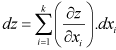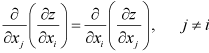Hence,

1.76

This is the condition of an exact (perfect) differential. If x and y are two independent thermodynamic properties, then Z (or z) will be also a thermodynamic property provided it satisfy Eq. (1.76). For example, let us consider the following relation,

dz = p dv + v2 dp

1.77

Here, M = p and N = v²

Now, and which does not satisfy Eq. (5.76). Hence Z is not a thermodynamic property.

Let us consider another relation,

z = p dv + v dp

1.78

With similar reasoning it can be easily established that Z is a thermodynamic property in this case.

With more than 3 variables, say x₁, x₂, x₃ and Z,

Z=(x1, x2, x3)

1.79

1.80

For dz to be an exact differential,

1.81

For k number of variables

1.82

or,

1.83