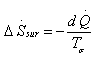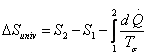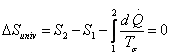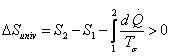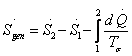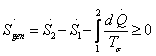Closed system

Consider a fixed mass of a substance in a closed system.

Entropy of any closed system can increase in two different ways

1. By heat interaction
2. By internal irreversibility or dissipative effects in which work or kinetic energy is dissipated into internal energy increase.

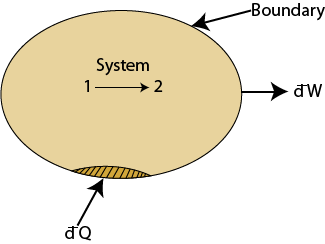
Fig. 1.16 A Closed System

Let, be an infinitesimal amount of heat transfer rate from surroundings to the closed system at the location on the boundary where temperature is T_σ. Let, be the rate of work transfer due to this heat transfer to the system.
Now, rate of entropy change of the surroundings is

1.41

If heat transfer does occur in many locations of the boundary we can write the entropy transfer due to heat transfer as for the accomplishing the process within the system from state 1 to state 2.
Entropy change of the system is

1.42

Taking the system and surroundings together, entropy change of the universe is

1.43

or,

1.44

For a reversible process

1.45

For an irreversible process

1.46

By definition

1.47

Thus for a closed system

1.48

or,

1.49

or,

1.50

where S₂ - S₁ = entropy change between two equilibrium states

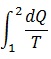           = entropy transfer

          S_gen = entropy production between the two equilibrium states

∴ Sgen ≥ 0

1.51

Second Law of thermodynamics states that, in general any thermodynamics process is accompanied by entropy generation.