The complete procedure may be summarized as follows:
1. Calculate 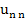 and and 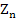 , starting with , starting with 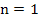 , from the relations : , from the relations :

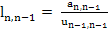
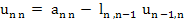

The quantities 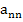 need not be saved, unless the same system is solved repeatedly for different non–homogeneous terms. The quantities need not be saved, unless the same system is solved repeatedly for different non–homogeneous terms. The quantities 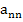 and and  are not used after are not used after 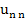 and and 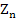 have been computed. have been computed.
2. Calculate 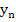 , stating with , stating with 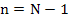 , form the relations: , form the relations:
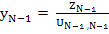
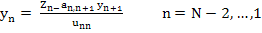
The whole process requires approximately 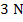 additions, additions, 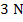 multiplications and multiplications and 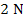 divisions. This compares very favorably to the divisions. This compares very favorably to the 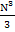 multiplications alone that have to be performed in the solution of a system with a matrix of order multiplications alone that have to be performed in the solution of a system with a matrix of order 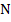 that has no zero elements. that has no zero elements.
Solution of the difference scheme: nonlinear case.
If the function 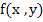 is not linear in is not linear in 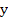 , one can not hope to solve the system (10.27) by algebraic methods. Some iterative procedure must be resorted to. The method which is recommended for this purpose is generalization of the Newton-Raphson method to systems of transcendental equations. , one can not hope to solve the system (10.27) by algebraic methods. Some iterative procedure must be resorted to. The method which is recommended for this purpose is generalization of the Newton-Raphson method to systems of transcendental equations.
In the case of a single equation, the Newton-Raphson method consists of linearizing the given function 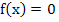 by replacing by replacing 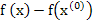 by its differential at a point by its differential at a point 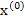 believed to be close to the actual solution, and solving the linearized equation believed to be close to the actual solution, and solving the linearized equation 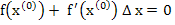 . The value . The value 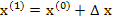 is then accepted as a better approximation, and the process is continued if necessary. Quite analogously if is then accepted as a better approximation, and the process is continued if necessary. Quite analogously if 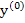 is a vector believed to be close to the actual solution of the equation is a vector believed to be close to the actual solution of the equation
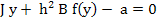 |
(10.44) |
so that the residual vector
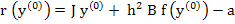 |
(10.45) |
is small, we replace the increments of the function 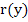 by their differentials at the point by their differentials at the point 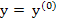 and solve the resulting linear system of equations for the increment of the vector and solve the resulting linear system of equations for the increment of the vector 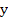 , which we shall call by , which we shall call by 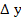 . Since the expression . Since the expression 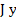 is already linear in is already linear in 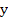 , the differential of the vector , the differential of the vector 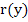 at at 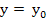 is found to be is found to be 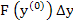 , where , where 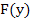 denotes the diagonal matrix denotes the diagonal matrix
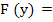  |
(10.46) |
|