Now writing 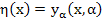 , we obtain , we obtain
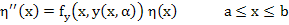 |
(10.19) |
From the definition of 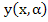 , we have , we have
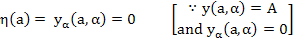
and
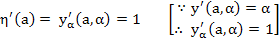 |
(10.20) |
We shall show that
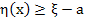 for for 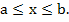
Assume that
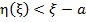 for some for some 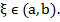
Since 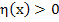 for small positive values of for small positive values of 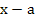 , we may assume without loss of generality that , we may assume without loss of generality that
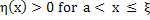 |
(10.21) |
By the mean value theorem,
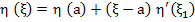 for some for some 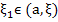
or 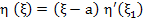 for for 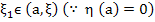
it follows that
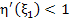 (because of the assumption that (because of the assumption that 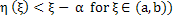 . .
Applying the mean value theorem to the function 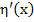 , we have , we have
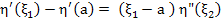 for some for some 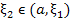 . In view of . In view of 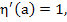 we then have we then have 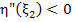 (because (because 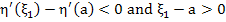 ). This contradicts the differential equation (10.19) in view of ). This contradicts the differential equation (10.19) in view of 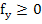 and (10.21). It thus follows that and (10.21). It thus follows that 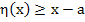 . The desired relation (10.18) is the special ease . The desired relation (10.18) is the special ease 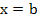 . .
|