Existence of a unique solution:
The main motivation for concentrating on problems of class 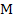 is the following theorem: is the following theorem:
Theorem: A boundary value problem of class 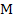 has a unique solution. has a unique solution.
Proof: Let 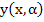 denote the solution of the initial value problem denote the solution of the initial value problem
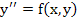
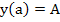
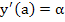 . .
By virtue of a standard theorem in the theory of differential equation (theorem 7.5 of chapter 1 in Coddington and Leuinson), 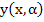 is a continuous function of is a continuous function of 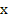 and and 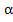 , and , and 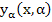 also exists and is continuous for also exists and is continuous for 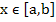 and all values of and all values of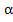 . .
In order to show that the equation for 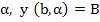 , has exactly one solution, we shall prove that , has exactly one solution, we shall prove that
 |
(10.18) |
The desired result then follows from the fact that a monotone function defined for all values of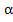 whose derivative is bounded away from zero assumes every value exactly once. whose derivative is bounded away from zero assumes every value exactly once.
In order to establish (10.18), we differentiate the identity

with respect to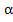 . We get . We get
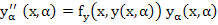
|