Proof: we have
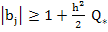
But if 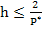 , then , then
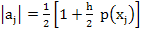
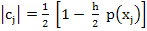
and so 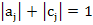 . .
Thus the difference system is strictly diagonally dominant and the result follows.
Truncation error
To estimate the error in the numerical solution of BVP by finite difference method we first define the local truncation error 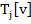 in in 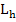 , as an approximation to L, for any smooth function , as an approximation to L, for any smooth function 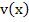 , by , by
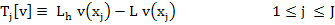 . .
If 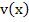 has continuous fourth derivatives on has continuous fourth derivatives on 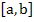 , then , then
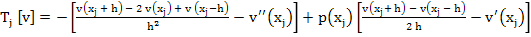
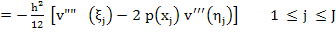 . .
Here 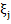 and and 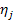 are values in are values in 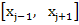 . .
Thus we find that 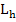 is consistent with L i.e. is consistent with L i.e. 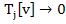 as as 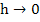 for all factors for all factors 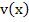 having a Cont. second derivative on having a Cont. second derivative on 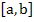 . Further . Further 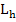 has second order accuracy. has second order accuracy. |