Uniqueness
We shall first show that the difference system obtained above has a unique solution.
Theorem: Let the element of A satisfy

Then A is non singular and the quantities 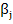 and and 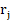 are bounded by are bounded by
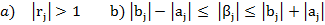
Proof: If 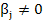 for for 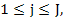 the factorization the factorization 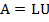 is valid. Then is valid. Then 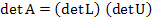
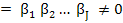 so that A is nonsingular so that A is nonsingular
From the hypothesis, 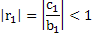 . .
For an inductive proof of (a), assume that 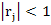 for for 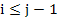 . But we know that . But we know that
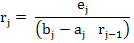
and thus  , so part a) follows. Now we use , so part a) follows. Now we use 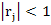 in in 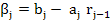 and take absolute values to conclude part (b). and take absolute values to conclude part (b).
Cor. Let 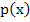 and and 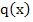 satisfy the inequalities satisfy the inequalities 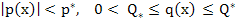
and the mesh spacing 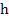 satisfy satisfy
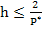 . Then the finite difference system has a unique solution. . Then the finite difference system has a unique solution.
|