We know that the 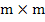 linear systems linear systems
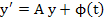
where the matrix A has distinct eigen values 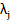 and corresponding eigen vector and corresponding eigen vector 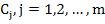 has a general solution of the form has a general solution of the form
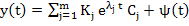
Let us assume that 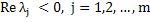 then the term then the term 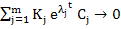 as as 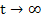 we therefore call this term the transient solution, and call the remaining term we therefore call this term the transient solution, and call the remaining term 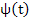 the steady state solution. Let the steady state solution. Let 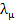 and and 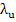 be two eigen values of A such that be two eigen values of A such that
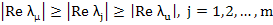
If our aim is to find numerically the steady state solution 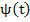 , then we must pursue the numerical solution until the slowest decaying exponential in the transient solution, namely , then we must pursue the numerical solution until the slowest decaying exponential in the transient solution, namely 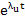 is negligible. Thus, the smaller is negligible. Thus, the smaller 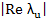 , the longer will be the range of integration. On the other hand, the presence of eigen values of A far out to the left in the complex plane will force us to use excessively small step lengths in order that , the longer will be the range of integration. On the other hand, the presence of eigen values of A far out to the left in the complex plane will force us to use excessively small step lengths in order that 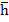 will lie within the range of absolute stability of the method. The further out such eigen values lie, the more severe is the restriction on step length. A rough measure of this difficulty is the magnitude of will lie within the range of absolute stability of the method. The further out such eigen values lie, the more severe is the restriction on step length. A rough measure of this difficulty is the magnitude of 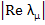 . If . If  , we are forced into the highly undesirable computational situation of having to integrate numerically over a long range, using a step length which is everywhere excessively small relative to the interval, this is the problem of stiffness. We can make the following somewhat heuristic definition. , we are forced into the highly undesirable computational situation of having to integrate numerically over a long range, using a step length which is everywhere excessively small relative to the interval, this is the problem of stiffness. We can make the following somewhat heuristic definition. |