If we now attempt to solve this problem by Euler's method with 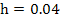 in the range in the range 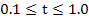 with with 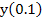 given by the exact solution. We find that for the given problem in the range given by the exact solution. We find that for the given problem in the range 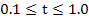 , the choice of , the choice of 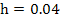 causes causes 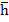 to lie outside the region of absolute stability, which is the circle to lie outside the region of absolute stability, which is the circle 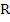 with center with center  radius 1, and it follows that for radius 1, and it follows that for 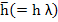 to lie within to lie within 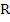 for all three values of for all three values of 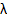 , we must satisfy , we must satisfy 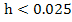 . Note that the eigen values responsible for this severe restriction in . Note that the eigen values responsible for this severe restriction in 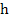 are are 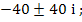 that is, the very eigen values whose contributions to the theoretical solution are negligible in the range that is, the very eigen values whose contributions to the theoretical solution are negligible in the range 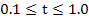
On the other hand, consider the IVP
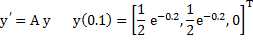
where 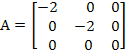
whose theoretical solution 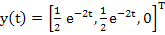
is, in the range 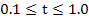 , virtually indistinguishable from that of the previous problem, is integrated perfectly satisfactorily by Euler's rule with step length , virtually indistinguishable from that of the previous problem, is integrated perfectly satisfactorily by Euler's rule with step length 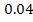 . The Eigen values of the system for this problem are . The Eigen values of the system for this problem are 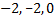 and for absolute stability we require only and for absolute stability we require only 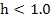 . . |