| |
Clearly 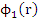 has degree at most has degree at most 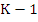 . Then by a theorem of Schur . Then by a theorem of Schur 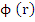 is a Schur polynomial if and only if is a Schur polynomial if and only if 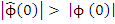 and and 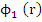 is a Schur polynomial. is a Schur polynomial.
Clearly, the interval 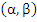 is an interval of absolute stability if, for all is an interval of absolute stability if, for all 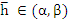 the (real) stability polynomial the (real) stability polynomial 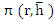 , is a Schur polynomial. Writing , is a Schur polynomial. Writing 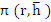 for for 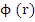 , we can construct , we can construct 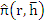 and and 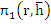 . The first condition . The first condition 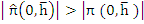 yields our first inequality in yields our first inequality in 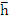 , while the second condition may be tested by writing , while the second condition may be tested by writing 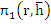 for for 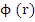 and repeating the process, there by obtaining a second inequality for and repeating the process, there by obtaining a second inequality for 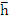 , and so on. At each stage, the degree of the polynomial under test in reduced by one, so that eventually we merely have to state a criterion for a polynomial of degree one to be a Schur polynomial, and, obviously, this can easily be done. , and so on. At each stage, the degree of the polynomial under test in reduced by one, so that eventually we merely have to state a criterion for a polynomial of degree one to be a Schur polynomial, and, obviously, this can easily be done.
We cannot use the Schur criterion directly to determine intervals of relative stability is the sense previously defined. However, if we adopt a definition of relative stability which requires that 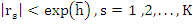 , then it is technically possible to use the Schur criterion. Substituting , then it is technically possible to use the Schur criterion. Substituting 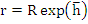 into (8.34) gives a polynomial equation in into (8.34) gives a polynomial equation in 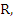
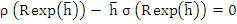
If the roots of this equation are 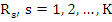 , then the Schur criterion gives necessary and sufficient conditions for , then the Schur criterion gives necessary and sufficient conditions for 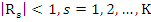 , that is, for , that is, for 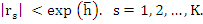 |