1. Root Locus Method
The first and most direct-method is the root locus method . This consists of repeatedly solving the polynomial equation (8.34) for a range of values of 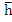 in the neighborhood of the origin. Any standard numerical method, such as Newton-Raphson iteration, may be employed for the approximate solution of (8.34). A plot of in the neighborhood of the origin. Any standard numerical method, such as Newton-Raphson iteration, may be employed for the approximate solution of (8.34). A plot of 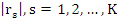 against against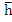 then allows us to deduce intervals of stability in the neighborhood of the origin. then allows us to deduce intervals of stability in the neighborhood of the origin.
2. Schur Criteria
We shall call the second method we consider the Schur criterion. In fact, several criteria based on theorem of Schur have been proposed unstably the Wilf stability criterion.
We state the criterion for a general 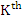 degree polynomial, with complex coefficients degree polynomial, with complex coefficients
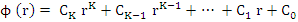
where 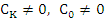 . The polynomial . The polynomial 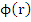 is said to be a Schur polynomial if its root is said to be a Schur polynomial if its root 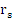 satisfy satisfy 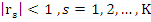 . Define the polynomials . Define the polynomials
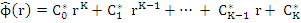
where 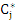 is the complex conjugate of is the complex conjugate of 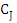 and and
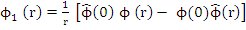 . .
|