Method not absolutely stable but relatively stable :
Example: Consider, for example, Simpson's rule which, being an optimal method, turns out to have no interval of absolute stability. A method is said to be an optimal method, if its order is 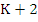 , where K is the step number of the method. The Simpson's rule is , where K is the step number of the method. The Simpson's rule is
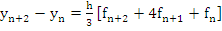 . .
For this method, we have
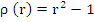
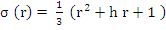
And the stability polynomial is
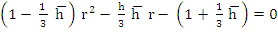
It is easily established that the roots 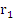 and and 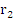 of this equation are real for all values of of this equation are real for all values of 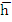 . Using . Using 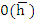 approximation of the roots, we can take approximation of the roots, we can take
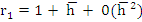 . The spurious root of . The spurious root of 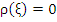 is is 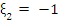 and so we write, and so we write,
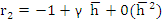 . Substituting this value in the stability polynomial gives . Substituting this value in the stability polynomial gives 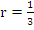 . For sufficiently small . For sufficiently small 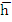 , we can ignore , we can ignore 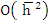 and have and have 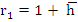 and and 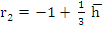 . .
This gives that the method is not absolutely stable but is relatively stable for 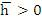 . .
|