This equation may be written in terms of first and second characteristic polynomial as
 |
(8.34) |
where

The polynomial  is frequently referred to as the characteristic polynomial of the method. However, we shall call is frequently referred to as the characteristic polynomial of the method. However, we shall call  the stability polynomial of the method defined by the stability polynomial of the method defined by  and and  . .
Definition: The linear multistep method (8.26) is said to be absolutely stable for a given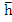 if, for that if, for that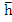 , all the roots , all the roots  of of  satisfy satisfy  , and to be absolutely unstable for that , and to be absolutely unstable for that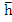 otherwise. An interval otherwise. An interval  of the real line is said to be an interval of absolute stability if the method is absolutely stable for all of the real line is said to be an interval of absolute stability if the method is absolutely stable for all  . If the method is absolutely unstable for all . If the method is absolutely unstable for all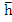 it is said to have no interval of absolute stability. it is said to have no interval of absolute stability.
Definition: The linear multistep method (8.26) is said to be relatively stable for a given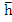 if for that if for that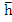 , the roots of , the roots of  satisfy satisfy  and to be relatively unstable otherwise. An interval and to be relatively unstable otherwise. An interval  of the real line is said to be an interval of relative stability if the method is relatively stable for all of the real line is said to be an interval of relative stability if the method is relatively stable for all  . . |