Stability Polynomial
Consider the general linear multistep method
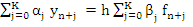 |
(8.26) |
which we assume to be consistent and zero–stable. The theoretical solution 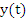 of the initial value problem satisfies of the initial value problem satisfies
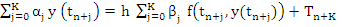 |
(8.27) |
where  , the local truncation error. If we denote by , the local truncation error. If we denote by 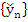 the solution of (8.26) when a round-off error the solution of (8.26) when a round-off error 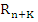 is committed at the is committed at the 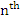 application of the method, then application of the method, then
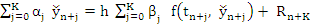 |
(8.28) |
on subtracting (8.28) from (8.27) and defining the global error 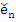 by by 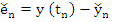 we find we find
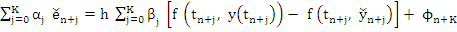 |
(8.29) |
where 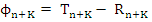
If we assume that the partial derivatives 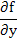 exists for all t exists for all t 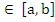 , then by the mean value theorem, there exists a number , then by the mean value theorem, there exists a number 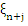 lying in the open interval whose end points are lying in the open interval whose end points are 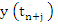 and and 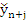 , such that , such that
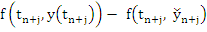
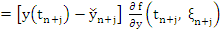
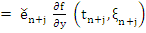
|