| |
The notion of a well posed problem is related to the more common notion of stability as indicated by the following definition.
Definition: Consider the differential equation 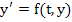 and without loss of generality, let the origin and without loss of generality, let the origin 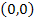 be an equilibrium point, i.e. be an equilibrium point, i.e. 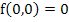 . Then the origin is: . Then the origin is:
- Stable, if a perturbation of the initial condition
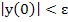 grows no larger than grows no larger than 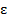 for subsequent times, i.e. if for subsequent times, i.e. if 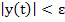 for for 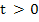
- Asymptotically Stable, if it is stable and
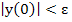 implies that implies that
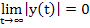
grows no larger than 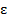 for subsequent times, i.e. if for subsequent times, i.e. if 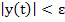 for for 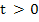
- Unstable if it is not stable.
Remark: This definition could also involve perturbations of 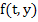 , which are omitted for simplicity. , which are omitted for simplicity.
An autonomous system is one where 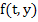 does not explicitly depend on t, i.e. does not explicitly depend on t, i.e. 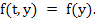
If 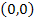 is an equilibrium point then, in this case, is an equilibrium point then, in this case, 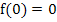 . Expanding the solution in a Taylor's series, we have . Expanding the solution in a Taylor's series, we have
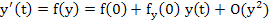
Since 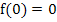 , we have , we have
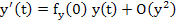
|