Some Special Methods:

Let us consider the differential equation

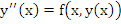(7.35)

By integrating twice, we obtain the formula

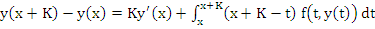(7.36)

which also may be regarded as a form of Taylor's formula with a remainder term. This result is not yet satisfactory for our proposes, because we do not wish to use the first derivative 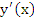. However, by writing down the same result with K replaced by –K and adding, the first derivative drops out, and the sum of the two integrals, writing 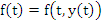, may be transformed as follows:

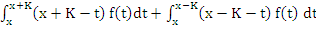
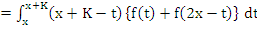
(This is obtained by putting 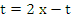in the second integral).