Introduction:

In the earlier section, we have discussed multistep methods for a single differential equation, but these methods can also be generalized to systems of differential equations. It is thus possible, for instance, to integrate a differential equation of the second order,

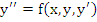(7.32)

by reducing it to the system

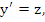
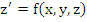(7.33)

and applying one of the methods described earlier. As in the case of one-step methods, this procedure is a perfectly legitimate one. No accuracy is lost, nor is there any unnecessary outlay of computational effort.

The situation is slightly different if the equation to be integrated is of the form

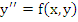(7.34)

i.e., if no derivatives appear in the right hand member of the differential equation. Equations of this type will be called special differential equations, and so will those of the form 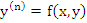where n is an integer . Special differential equations of the second order, and in particular systems of such equations, occur frequently, e.g., in mechanical problems without dissipation. If one is not particularly interested in the values of the first derivatives, it seems unnatural to introduce them artificially in order to produce systems of first order equations. This section is, however, denoted to the study of the methods which deal directly with such type of equations.