This is the desired expression for the remainder in the Adams-Bashforth formula.
In a completely analogous manner, we find for the Adams-Moulton formula
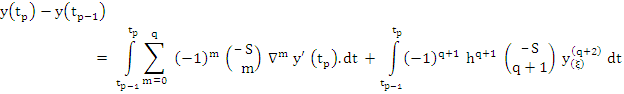
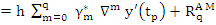 |
(7.26) |
where
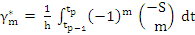
and
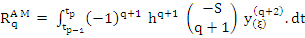
The Adams-Moulton formula is obtained by neglecting the remainder term 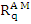 in (7.26). Again, we use the following two facts about in (7.26). Again, we use the following two facts about 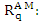
-
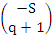 is of constant sign in the interval is of constant sign in the interval 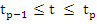 and and
-
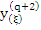 is a continuous function of is a continuous function of 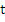 . .
Thus applying second mean value theorem of integral calculus, we have
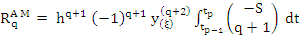
for some  satisfying satisfying 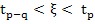 . By definition of . By definition of 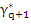 , we have , we have
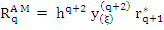 |
(7.27) |
|