where 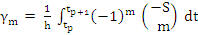
and
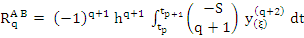
The Adams-Bashforth formula is obtained by neglecting the term 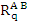 in (7.24) and is given as in (7.24) and is given as
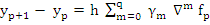
we now make use of the following two facts about 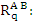
-
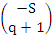 is of constant sign in the interval is of constant sign in the interval 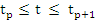 and and
-
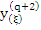 is a continuous function of is a continuous function of 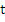 . We are thus in a position to apply the second mean value theorem of the integral calculus with the result that . We are thus in a position to apply the second mean value theorem of the integral calculus with the result that
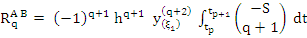
where 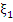 is one of the values of is one of the values of  corresponding to values of corresponding to values of 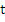 in in 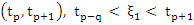 . By the definition of . By the definition of 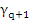 , this may be written as , this may be written as
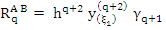 |
(7.25) |
|