Necessary and Sufficient condition for Convergence
We shall now study the necessary and sufficient condition for convergence of a general one-step method which is given in the following theorem:
Theorem: If 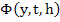 is continuous in is continuous in 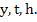 for for 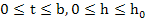 and all and all 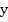 , and if it satisfies a Lipschitz condition in , and if it satisfies a Lipschitz condition in 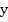 in that region, a necessary and sufficient condition for convergence is that in that region, a necessary and sufficient condition for convergence is that
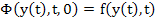 |
(5.4) |
Remark: The equation (5.4) is called the condition of consistency. Since, by suitable choice of initial conditions, 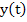 can take on any value for a given can take on any value for a given 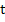 , the equation (5.4) will hold for any , the equation (5.4) will hold for any 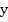 in the form in the form
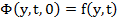
Proof: Let 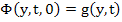
Since 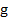 satisfies the conditions of existence and uniqueness of the solution, the IVP satisfies the conditions of existence and uniqueness of the solution, the IVP
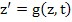
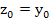 |
(5.5) |
has a unique differentiable solution. We shall show that the numerical solution given by (5.1) converges to 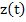 , and hence , and hence 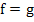 is a necessary and sufficient condition. is a necessary and sufficient condition. |