Remark: For all one-step explicit methods, the bound for the principal local truncation error is also a bound for the whole local truncation error. In view of this, we may write
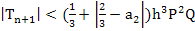 |
(3.40) |
as the bound (Lotkin) for the local truncation error for a two-stage Runge-Kutta method.
In the case of general three stage and four stage Runge-Kutta methods, the bound for the local truncation error is very complicated. For the classical fourth order Runge-Kutta method (3.30) the bound for the local truncation error (using Lotkin's bounds) is given by
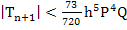 |
(3.41) |
For the general explicit one-step method (3.11), the bound for the global truncation error is an order of magnitude greater than the bound for the local truncation error. If the local truncation error 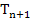 defined by (3.32) satisfies defined by (3.32) satisfies
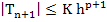 |
(3.42) |
where K is a constant, then the global truncation error
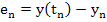
satisfies the inequality
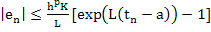 |
(3.43) |
where 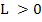 is the Lipschitz constant of is the Lipschitz constant of 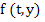 with respect to y. with respect to y. |