Lotkins Bounds
We can find a bound for 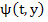 if we assume that the following bounds for f and its partial derivatives hold for if we assume that the following bounds for f and its partial derivatives hold for 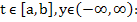
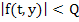
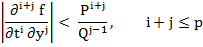 |
(3.37) |
Where P and Q are positive constants and p is the order of the method. These bounds are due to Lotkin and are called Lotkin's bounds. Here in this example, we have
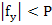
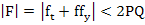
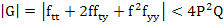
Hence from (3.36), we have
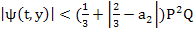 |
(3.38) |
and we obtain the following bound for the principal local truncation error:
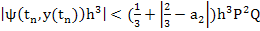 |
(3.39) |
|